各种激活函数的介绍

常见激活函数的介绍

激活函数的作用

1. 把神经元的输出拉回在一定范围内.
2. 给模型添加非线性因素. 因为线性模型的表达能力不够, 多层线性叠加还是线性, 相当于一层网络$y=Mx+b$. 但是有些模型只使用线性函数是无法表示的.

比如下面这个简单的图, 想用一个函数把蓝色和红色分开, 只使用直线无法分开, 需要添加非线性因素: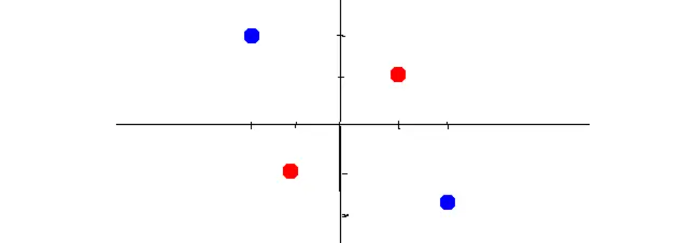

什么是线性函数:

首先理解下‘线性函数’这个基本概念, 之所以想强调这点, 是因为在一次面试时面试官问我“Relu激活函数是两条射线构成, 为什么不是线性函数?” 我当时没回答出来-.-

线性函数是一种线性映射, 是能维持向量加法和标量乘法的映射. 也就是能满足以下公式的$f(x)$是线性函数:

$$f(x+y) = f(x) + f(y) \\ f(\alpha x) = \alpha f(x)$$

其中$\alpha$是标量, x和y是向量.

之所以强调x和y是向量, 我们看下面这个例子: 假设现在有

$$f(x) = 2x+3$$

这个函数f(x)是线性函数, 但是: $f(2x)=2(2x)+3=4x+3$, $2f(x)=2(2x+3)=4x+6$, 显然$f(2x)!=2f(x)$, 为什么这个函数是线性函数, 却不满足标量乘法呢?

如果只是单纯的把变量x考虑为标量, 确实$f(2x)!=2f(x)$, 但是这里输入的变量x是向量, 判断向量相等的条件是: 方向相同且长度相等. 如果从向量角度看, 是满足$f(2x)==2f(x)$的.

这里输入向量x是$x=[x_1]$, 即只有一个标量$x_1$的1*1大小的向量. $f(2x)=2(2x)+3=4x+3$表示把向量的长度扩大四倍后向右平移3格, $2f(x)=2(2x+3)=4x+6$表示把向量长度扩大四倍后向6平移6个. 所以从向量的角度看, 最后得到的向量都是通过向量4x平移得到, 方向相同且长度相同, 满足$f(2x)==2f(x)$.

ReLu激活函数不是线性函数
ReLu公式: $f(x)=Max(x,0)$, 如何判断这个f(x)是否为线性的?
首先看其是否满足标量乘法$f(\alpha x) = \alpha f(x)$: x小于0时都是0相等, x大于0时$f(x)=x$, $f(\alpha x)=\alpha x = \alpha f(x)$ 相等. 所以满足标量乘法.
下面看是否满足向量乘法$f(x+y) = f(x)+f(y)$: 如果$x=2$ $y=-2$, $f(x)=2$, $f(y)=0$, $f(x+y)=f(0)=0$, $f(x+y)!=f(x)+f(y)$, 不满足向量乘法.
所以ReLu激活函数是非线性.

常见激活函数

sigmoid函数

$$f(x)= \frac{1}{1+e^{-x}}$$

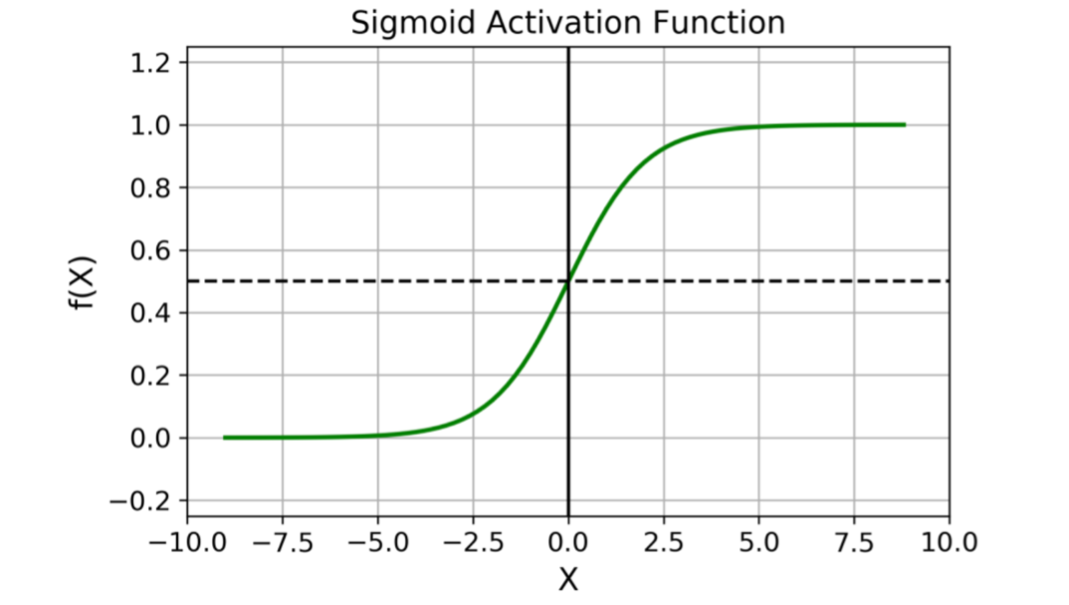
输出值在0~1之间, 对每个神经元的输出进行归一化. 一般地, 二元分类问题会用sigmoid作为输出层.

sigmoid缺点:

• 容易梯度消失;
• 指数运算, 速度慢;
• 输出不是以0为中心;

softmax函数

$$Softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^C e^{x_j}}$$

softmax是sigmoid在多分类上的推广, softmax可以用在多分类问题的最后一层.

单个输出节点的二分类问题一般在输出节点上使用Sigmoid函数，拥有两个及其以上的输出节点的二分类或者多分类问题一般在输出节点上使用Softmax函数。

tanh激活函数

$$f(x) = tanh(x) = \frac{2}{1+e^{-2x}} - 1$$

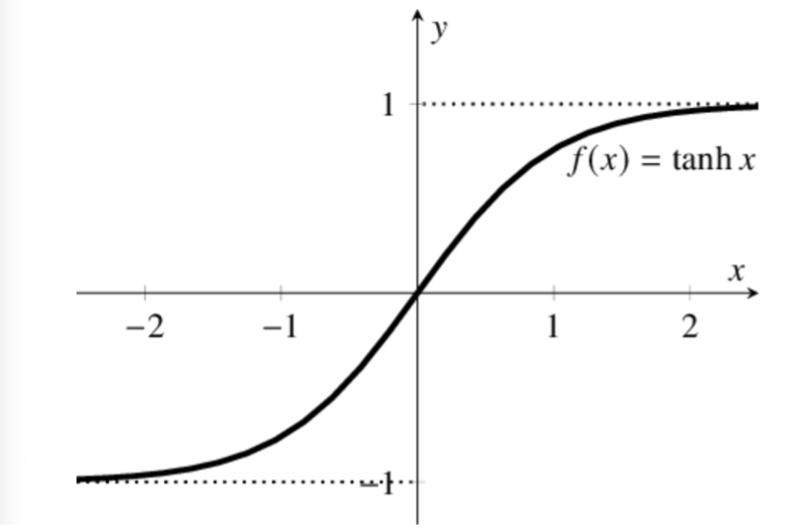
Relu激活函数

$$f(x)=max(x,0)$$

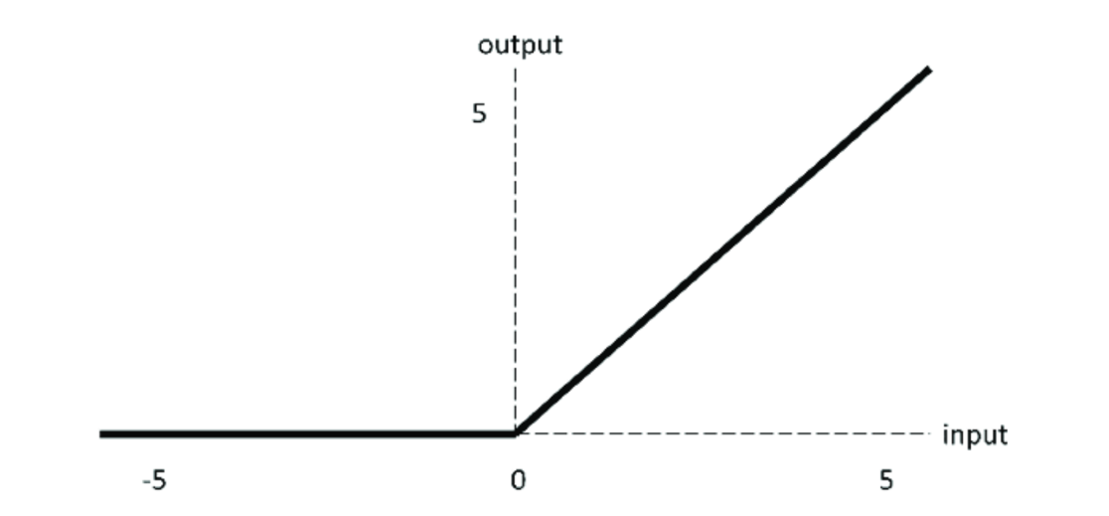
ReLU对小于0的值全部抑制为0；对于正数则直接输出，这是一种单边抑制的特性，而这种单边抑制来源于生物学。
在反向传播的过程中，它既不会放大梯度，造成梯度爆炸；也不会缩小梯度，造成梯度消失的现象。

优点：

1. 输入为正时，没有梯度饱和的问题。（就是导数趋近于0的问题）
2. 计算快，线性计算。
3. 增加网络的稀疏性，当x<0,输出为0，神经元为0的越来越多，网络稀疏，网络协同性被破坏，迫使网络学习更加一般性的特征，泛化能力变强。这也是dropout的原理。减少了参数的相互依存关系，缓解了过拟合问题的发生。和符合生物神经元的单边抑制性。

缺点：

1. 输出不是以0为中心。
2. relu还会有梯度爆炸的问题，因为上限是inf。
3. 输入为负数，relu失效，梯度完全为0，导致一些节点‘不可逆转的死亡’。
   如果开始选定的学习率比较大的话很可能40%的神经元在训练开始的时候就会”死亡”，因此使用ReLU激活函数的时候，需要选定一个合适的学习率让这种情况发生的概率降低；

relu在0处不可导怎么办:
我们可以人为提供一个伪梯度, 自己定义在0处的导数为0, 或者0~1之间的某个值.

Leaky Relu激活函数

$$f(x) = max(\alpha x, x), \ \alpha=0.01$$

Swish激活函数

$$f(x) = x * sigmoid(x) = \frac{x}{1+e^{-x}}$$

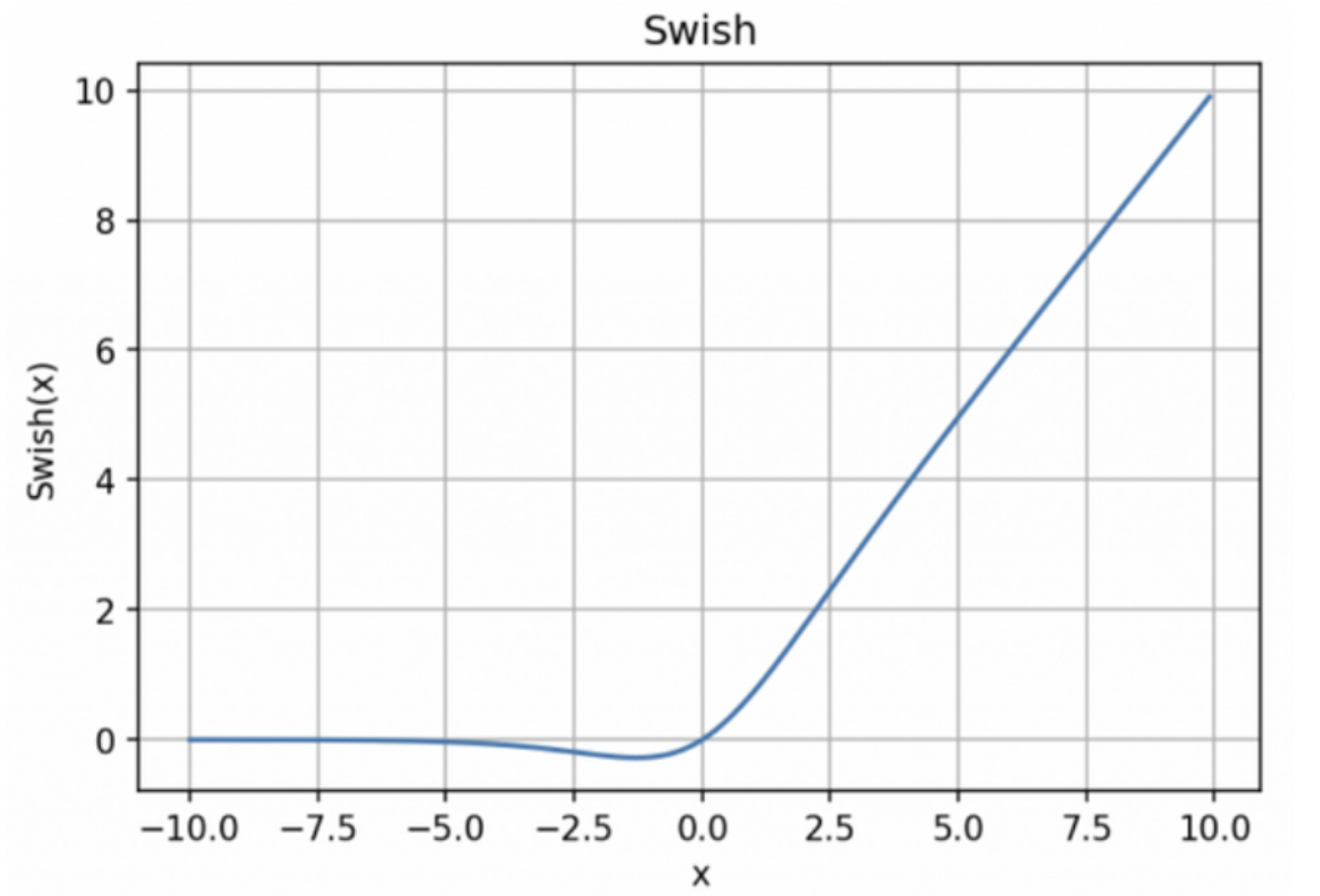
与 ReLU 相比，尽管图形非常相似，Swish 的性能却要稍好一些。然而，ReLU 在 x=0 时会突然发生改变，而 Swish 与此不同，它不会在某个点上突然改变，这使得训练时 Swish 更容易收敛。

但是，Swish 的缺点是它的计算成本很高。

ELU激活函数

$$f(x) = \begin{cases} x, \quad x \geq 0 \\ \alpha (e^{x}-1), \quad x<0 \end{cases}$$

GELU激活函数

GELU全称是Gaussian Error Linear Unit, 在transformer或者bert中很常用的激活函数. 公式:

$$GELU(x) = x * \Phi (x) = x * P(X\leq x)$$

近似数学公式:

$$GELU(x) = 0.5x(1+tanh(\sqrt{\frac{2}{\pi}}(x+0.044715x^3)))$$

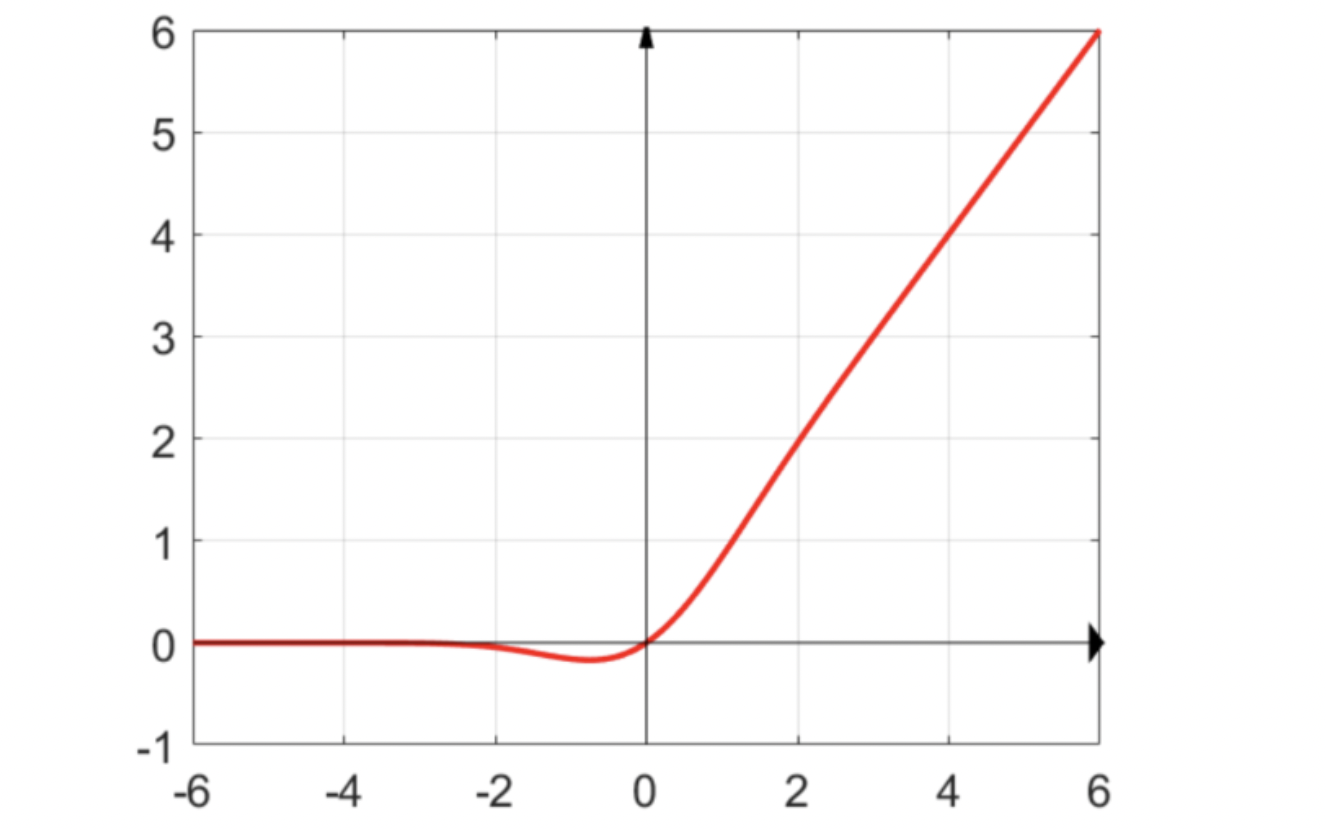
GELU的含义:
GELU可以看做dropout, relu, zoneout的综合, 对输入变量x乘以一个0和1组成的mask, 这个mask服从伯努利分布(即0-1分布):

$$mask=bernoulli(\Phi(x))=bernoulli(P(X\leq x))$$

其中输入的x服从正态分布, $\Phi(x)=P(X\leq x)$是x的累积分布函数, 即服从标准正态分布的累积分布函数. 因为神经元的输入x往往遵循正态分布, 存在batch normalization.

为何说GELU可以看做dropout, relu, zoneout的综合
RELU当x小于等于0是舍弃它, 当x大于0时保留; 而dropout会随机的给x乘上0; zoneout是RNN时间维度上的“dropout”，要么维持前一个时刻的hidden vector，要么按照一般的样子更新。

像RELU等分段线性函数在间断点不可导, 并且它们作为确定性非线性函数, 需要额外给网络引入随机正则化来提高模型的泛化性. 如果一个激活函数本身就具有随机正则性, 是不是就能同时保持模型的泛化性和非线性? 为此提出的GELU激活函数同时具有随机正则性和非线性.

因为GELU激活依赖于输入本身, 换句话说, 对x乘以0还是1取决于x自身. 输入的x越大, 累积分布函数$\Phi(x)$就越大, 表示mask更有可能为1, 被保留; 反之x越小, mask更有可能为0, 被丢弃.

激活函数的特点:

• 激活函数的输出最好是关于0对称, 这样梯度不会朝着特定方向移动.
• 计算成本要小.
• 要有可微性.
• 会存在梯度消失问题. 多层网络嵌套在一起, 链式求导法则, 意味着多个0~1之间的值相乘, 梯度会越来越小.
• 梯度饱和问题. 常见的激活函数例如sigmoid和tanh, 在自变量很小或者很大时, 函数曲线基本和x轴平行, 梯度变化很小, 导致模型训练很慢.