详细理解attention的原理

transformer中最重要的就是attention block。这里会详细理解各种类型的attention block：

1. 注意力机制attention
2. 自注意力机制 self-attention
3. 多头注意力机制 multi-head attention
4. 掩码注意力机制 masked multi-head attention
5. 交叉注意力机制 cross attention

1.Attention基本原理

transformer中的基本结构式self-attention，而在理解自注意力机制self-attention之前，需要理解什么是attention注意力机制。

Attention会有Source和Target两个集合，Source中的元素想像成一系列的数据对，而Target中有若干Query数据。
通过计算Query和各个元素Key的相似性，得到每个Key对应Value的权重系数，然后对Value进行加权求和，得到最终的Attention值。
本质上Attention机制是对Source中元素的Value值进行加权求和，而Query和Key用来计算对应Value的权重系数。

Attention分为三个阶段：

• 阶段1:Query与Key进行相似度计算得到权值
• 阶段2:对上一阶段的计算的权重进行归一化
• 阶段3:用归一化的权重与Value加权求和，得到Attention值

Attention和self-attention的区别：
Attention的Source和Target是不同的，比如机器翻译任务中，Source是翻以前的英文句子，Target是翻译后的中文句子。而self-attention的Source和Target是同一个。

Attention计算的是Source对Target的attention，而self-attention是Source内部元素之间或者Target内部元素之间发生的Attention机制，也可以理解为Target=Source这种特殊情况下的注意力计算机制。

简单而言，在self-attention中，Q和K和V是同源的，即这三个张量是通过输入张量X经过线性变化（分别乘以矩阵$W^q, W^k, W^v$）得到的。而attention的Q和{K,V}是不同源的。

self.attention就是自己和自己做相识度计算，句子中每个词和句子中其他词计算相识度，利用上下文增强目标词的表达。

2.Self-Attention基本原理

self-attention这个机制是在论文‘attention is all you need’中提出的：

NLP任务会输入一个句子，首先会通过tokenizer向量化，然后添加位置编码，得到这组向量：${a_1, a_2,…,a_n}$。 self-attention输入的就是这一组向量:${a_1, a_2,…,a_n}$，然后输出的是上下文关联的向量组:${b_1,b_2…}$.

为什么需要self-attention：
一个句子，每个单词的上下文很重要，因为相同的单词在不同的上下文里的意思不同，如何让每个token向量考虑它的上下文？最简单的是使用sliding window，比如输入的句子是’I saw a saw.’, 滑动窗口的size=3时，每相邻的三个单词（为了简单理解，把每个单词看作一个token）输入给FC层，让每个单词可以学习到相邻的三个单词的信息。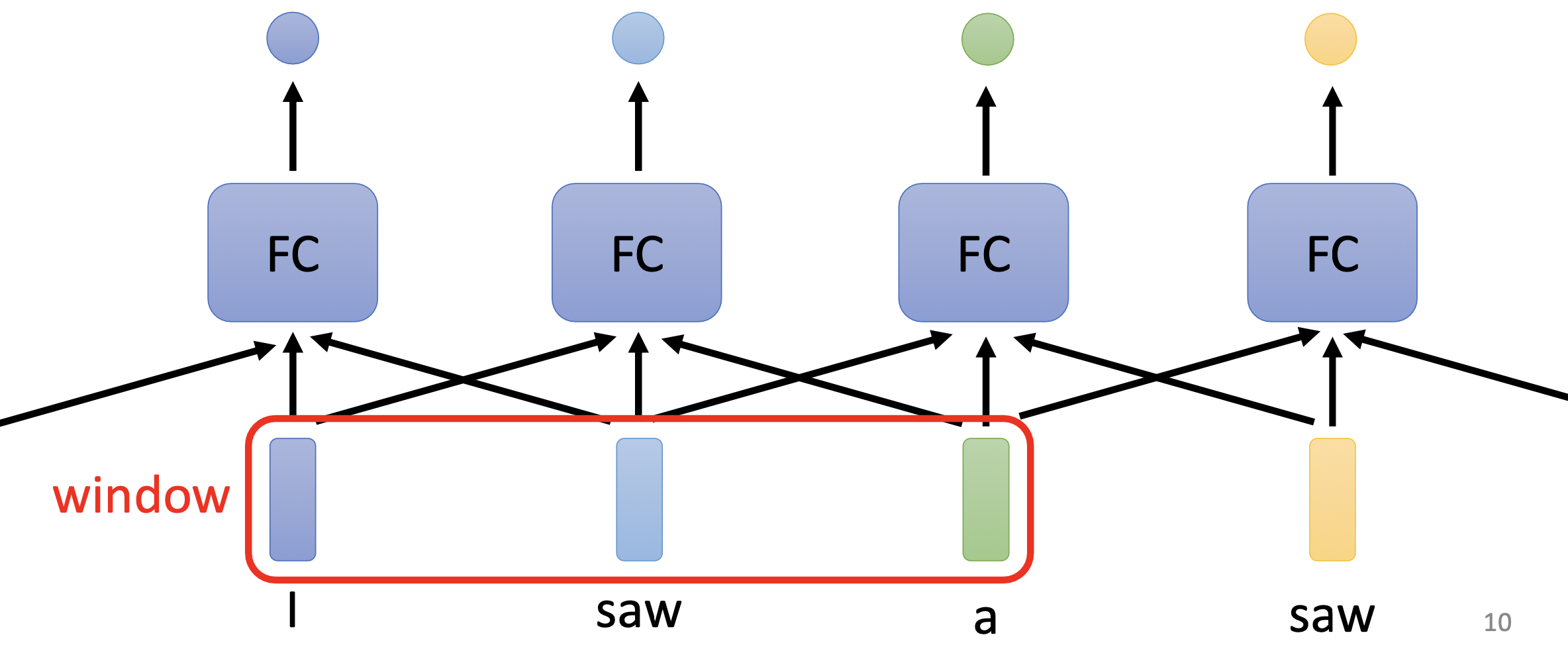

但是滑动窗口有局限性: 如果对某个单词想考虑整个句子的上下文，需要把window size调大覆盖整个句子吗？显然不现实，因为每个句子长度不同。而且window很长时，FC层（fully connected layer）的参数很多，难以训练。

为了让每个单词可以考虑上下文信息，这里提出了自注意力机制：输入一组向量${a_1, a_2,…,a_n}$，经过self-attention得到一组输出向量${b_1, b_2,…, b_n}$，为了方便理解假设输入的向量个数和输出的向量个数相等。
此刻，${b_i}$向量组中每个向量都是和整个句子上下文相关的，然后经过FC层和softmax得到预测概率。

自注意力机制如何让每个${b_i}$向量都和${a_i}$向量相关呢？具体实现如下：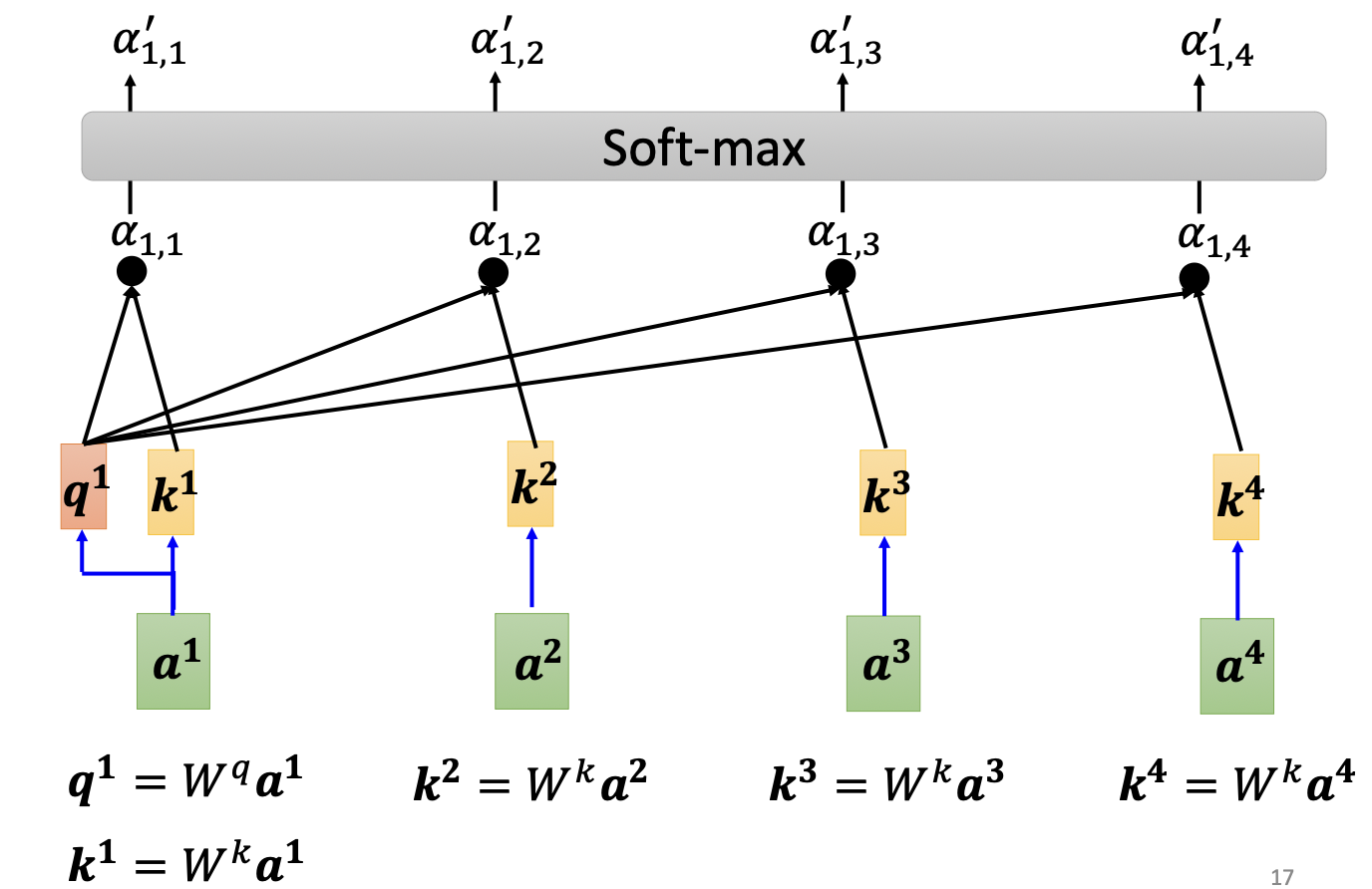

首先每个$a_i$向量和参数矩阵$W^q, W^k$相乘，得到$q_i, k_i$，然后$\alpha_{ij}=q_i*k_j$,经过softmax函数得到$\alpha’$：

$$\alpha'_{1,i} = \frac{exp(\alpha_{1,i})}{\sum_{j} exp(\alpha_{1,j})}$$

然后$\alpha’_{1,i}$和$v_i$相乘得到$b_1$: $b_1=\sum_i \alpha’_{1,i}v_i$.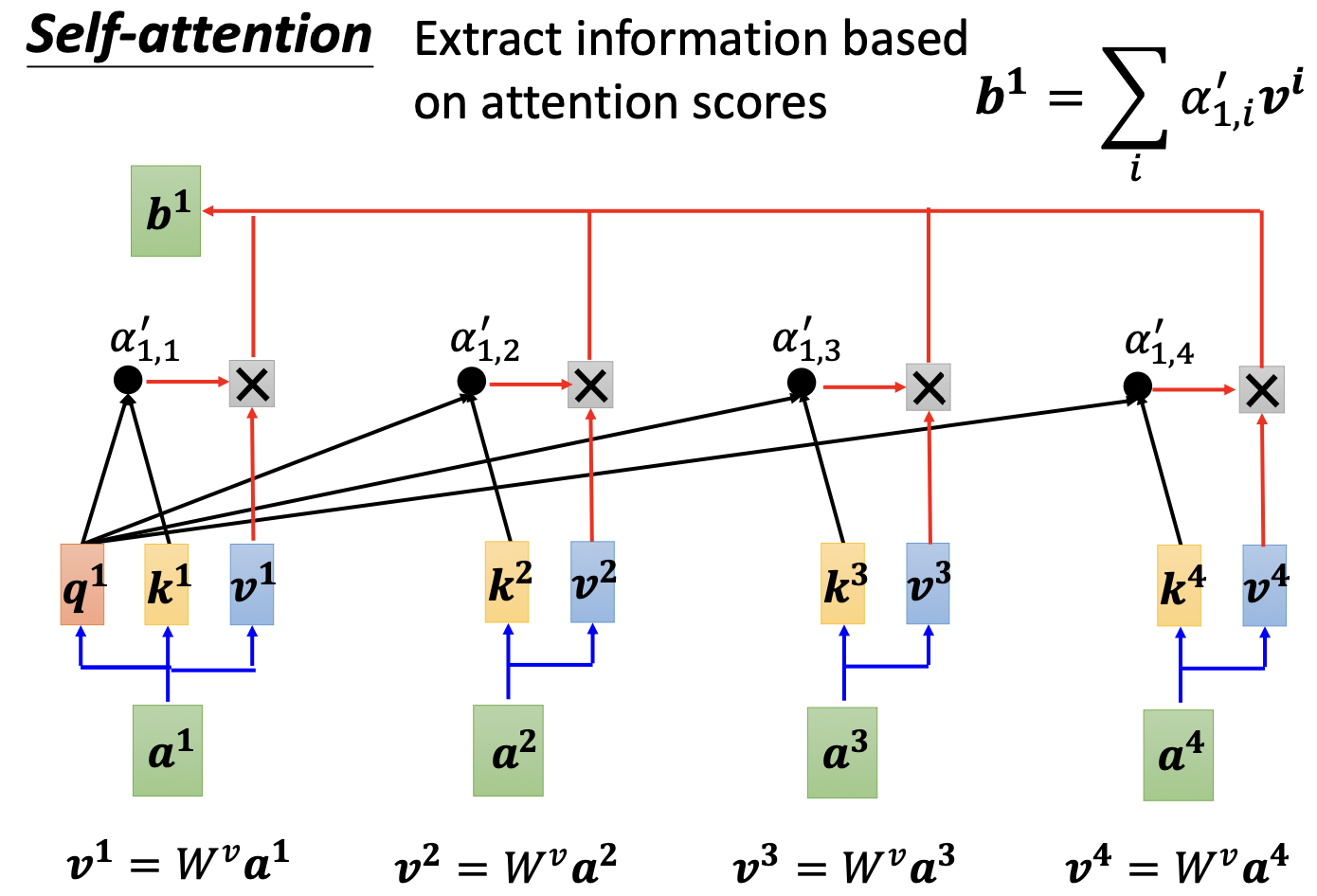

上面是把每个token向量的$q_i, k_i, v_i$向量单独看，但其实代码实现是直接把所有$q_i$向量合并看作$Q=[q_1,q_2,..q_n]$, K和V同理也是整个向量组的合并。
从整体张量分析，输入的张量$I=[a_1,a_2,..a_n]$,输出张量$O=[b_1,b_2…b_n]$:

上面通过流程图直观理解了attention的实现原理，然后我们就可以理解论文“attention is all you need”中的这个数学公式：

$$attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$

3.多头注意力机制 Multi-Head Attention

多头注意力机制，就是多个自注意力机制的结合。
直接看公式和流程图：

$$Q_i=QW_i^Q, K_i=KW_i^K, V_i=VW_i^V, i=1,2,..8 \\ head_i=Attention(Q_i,K_i,V_i) \\ MultiHead(Q,K,V)=Concat(head_1, head_2,...,head_8)W^O$$

之前每个输入向量$a_i$只会得到一组的${q_i,k_i,v_i}$，但是现在假设$n_head=8$，则每个$a_i$会得到8组的${q_{i,j},k_{i,j},v_{i,j}},j=1,2..8$，每一组q k v计算self-attention，然后得到的8组结果拼接起来乘以一个权重$W^O$.

4.掩码注意力机制

在decoder中会使用到掩码注意力机制。在上面的self-attention中，生成的$b_1$向量会考虑所有输入向量$a_i$，生成$b_2$也会考虑所有的$a_i$。
但是masked之后，生成$b_1$只考虑$a_1$, $b_2$只考虑$a_1,a_2$，生成$b_k$只考虑$a_1,a_2..a_k$。因为对decoder而言，是先有a1，再有a2 再有a3，一个一个产生的，不是一次性得到所有的ai。

5.交叉注意力机制

交叉注意力机制是混合两种不同嵌入序列的注意机制，两个序列必须具有相同的维度，两个序列可以是不同的模式形态（如：文本、声音、图像），一个序列（decoder序列）作为输入的Q，定义了输出的序列长度，另一个序列（encoder序列）提供输入的K和V。

Cross-attention的输入来自不同的序列，Self-attention的输入来自同序列，除此之外，基本一致。

Pytorch代码实现

上面介绍的各种注意力机制的原理，这里是pytorch实现的，结合这个代码可以更好理解注意力机制如何实现：
pytorch面试题：实现attention结构

参考：

吴恩达机器学习网课：https://speech.ee.ntu.edu.tw/~hylee/ml/2023-spring.php