优化器介绍II——动量和自适应学习率

本文最后更新于 2024年7月8日下午4点41分

优化器介绍II——动量&自适应学习率

在优化器篇章1 中，BGD/SGD/MBGD三种梯度下降方法的学习率是不变了，是提前设置好的超参数。这时就面临一个问题，如何设置初始学习率？因为使用不同的batch size时学习率最好有所变化。还有学习率在训练时不能自主调节吗（自适应学习率）？
下面介绍的这几种优化器，会使用动态调节的学习率。

什么是动量

一阶矩/二阶矩/一阶动量/二阶动量

首先简单介绍什么是一阶矩/二阶矩，一阶动量/二阶动量。我后面介绍的数学定义都是通俗理解的，为了方便看懂，不是严谨定义。
对一个向量$x=[x_1,x_2,..x_n]$，向量x的长度是$1 \times n$，x的均值和方差分别是：

$m=\frac{x_1+x_2+...+x_n}{n} \\ var = \frac{ (x_1-m)^2 + (x_2 - m)^2 + ...+(x_n-m)^2}{n}$

一阶矩：就是期望，就是平均值，对向量x的一阶矩就是对x求期望:

$E(x) = \frac{x_1 + x_2 + .. + x_n}{n}$

一阶中心距：就是对每个值$x_i$减去均值m再求期望:

$E(x-m) = \frac{(x_1-m) + (x_2-m)+...+(x_n-m)}{n}=0$

二阶矩：也是二阶非中心矩，对x的平方求期望,也是x的未中心化的方差:

$E(x^2) = \frac{x_1^2 + x_2^2 + ... +x_n^2 }{n}$

二阶中心矩：对变量x和均值m的差的平方求均值,二阶中心矩也叫做方差，它告诉我们一个随机变量x在它的均值附近波动的大小，方差越大波动越大:

$E((x-m)^2) = \frac{ (x_1-m)^2 + (x_2-m)^2 +...+(x_n-m)^2}{n} = var(x)$

现在有一个梯度张量$g=[g_1,g_2,..g_T]$, $g_t$是t时刻的梯度向量。
一阶动量：过去各个时刻的梯度的线性组合：

$\sum_{i=1}^T \alpha_i \times g_i = \alpha_1 g_1 + \alpha_2 g_2 +... + \alpha_T g_T$

二阶动量：过去各个时刻的梯度的平方的线性组合：

$\sum_{i=1}^T \alpha_i \times g_i^2 = \alpha_1 g_1^2 + \alpha_2 g_2^2 +... + \alpha_T g_T^2$

梯度的一阶矩：就是梯度g的期望: $E(g)$. 梯度的二阶矩，就是梯度的平方的期望，也是梯度的未中心化方差：$E(g^2)$.

鞍点

鞍点是一个非局部极值点的驻点，简单而言，鞍点在一个切面上是最小值，在一个切面上是最大值，图示如下：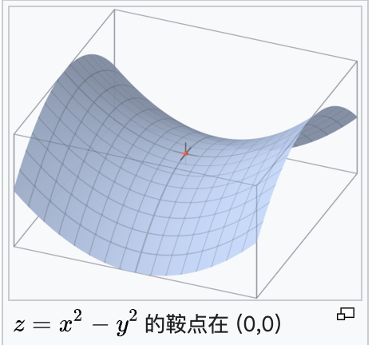
z=x^2-y^2的鞍点在(0,0)处

传统的随机梯度方法没有添加动量信息，为了解决SGD的山谷震荡和鞍点停滞问题，提出在参数更新时不仅仅有梯度，还有动量。假设现在有个重量几乎为0的小球，在山坡上滚下来，假设它没有惯性，只有速度没有加速度，通过山坡的切面来求速度：
山谷震荡：在山谷中，小球沿着山谷往下滚动，速度是切面梯度，两侧是山壁，则小球会在左右山壁来回碰撞，来回震荡的滚下来；
鞍点停滞：小球来到鞍点时，因为没有惯性没有加速度，来到鞍点的瞬间切面梯度=0所以速度=0，则小球会在鞍点停下来；
上面这个情况显然不符合物理规律因为没有惯性，如果把小球换成有重量的铁球，他有惯性，则铁球沿着山坡往下滚动时不容易被山壁弹来弹去，并且来到鞍点也会因为惯性继续向前。铁球更容易逃离鞍点找到全局最低点，而没有惯性的小纸球容易被困在鞍点或局部最优点。
小球滚下的轨迹图，左图不带惯性，右图带惯性

添加动量的梯度更新

上面这个场景形象解释了梯度更新.
传统的梯度更新是不带惯性的小纸球从山上滚下：当前时刻t的损失函数的梯度$g_t$=速度，学习率$\alpha$=时间，参数$\theta_{t+1}$=距离，看做一个距离公式:

$\theta_{t+1} = \theta_{t} - \alpha \times g_t \\ 距离_{new} = 距离_{old} - 时间 \times 速度$

添加了动量的是带惯性的铁球，添加了动量momentum的SGD叫做SGD with momentum，相当于添加了惯性. 这项$\beta v_{t-1}$就是动量或者惯性，公式如下：

$\theta_{t+1} = \theta_t - v_t, \ v_t = \beta v_{t-1} + \alpha g_t \\ 距离_{t+1} = 距离_{t} - 速度_t, \ 速度_t = 速度_{t-1} + 时间\times 加速度_{t}$

添加动量的特点：

下降初期，本来只有$g_t$梯度，现在添加了上一时刻的步伐$v_{t-1}$，$g_t$和$v_{t-1}$的下降方向一致，能加速参数更新。
下降中后期，在局部最小值来回震荡，此时的$g_t$很小，容易陷入鞍点/局部最小点，加上动量使得更新幅度增大，能跳出陷阱。
在梯度改变方向时（$v_{t-1}$和$g_t$的方向不一致），动量能减少更新（就像初速度向右，加速度向左，新速度会向右慢慢变小，然后向左加速，不会突然向左运动），抑制震荡。
总之，动量项能加速参数更新，抑制震荡，加快收敛。

AdaGrad优化器

下面看几个常见的添加了动量的优化器。
首先是AdaGrad优化器，它有自适应的学习率，能让不同参数有不同学习率。t和t+1是当前时刻和下一时刻，i是模型的第i个参数，$\eta$是初始的学习率，$\frac{\eta}{\sqrt{\sum_{k=0}^t g_{k,i}^2 + \epsilon }}$是自适应学习率：

$\theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{\sum_{k=0}^t g_{k,i}^2 + \epsilon }} g_{t,i}$

其中，这一项$- \frac{1}{\sqrt{\sum_{k=0}^t g_{k,i}^2 + \epsilon }}$也称为正则项，或者约束项regularize，$\epsilon$保证分母不为0。

AdaGrad优点：

适合处理稀疏梯度，在数据分布稀疏的场景，对稀疏参数用大的学习率，对非稀疏参数用小lr。历史梯度的平方和$\sum_{k=0}^t g_{k,i}^2$来表示参数的梯度的稀疏性。
- 如果$\sum_{k=0}^t g_{k,i}^2$很小,表示这个参数$\theta_i$稀疏不频繁出现，被更新的频率低，故用大步长更新它。
- 反之，如果$\theta_i$的$\sum_{k=0}^t g_{k,i}^2$大,表示其出现频繁，更新频繁，就用小步长更新它。
分母的求和实现了退火过程，随着时间推移，lr越来越小。保证算法的收敛。

缺点：

需要事先人工设置一个全局学习率$\eta$；
如果设置$\eta$过大，会让正则项很敏感，对梯度调节很大。
中后期，由于正则项的分母对梯度的累加，让梯度趋于0 训练提前结束。

RMSProp优化器

全称Root Mean Square Propagation，公式如下，其中$\eta$是初始化学习率：

$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{v_t}+\epsilon} g_t \\ v_t = \gamma v_{t-1} + (1-\gamma)g_t^2$

这个优化器为什么叫RMS，均方根？均方根就是变量x的平方的均值再开方。
我们注意到AdaGrad的约束项的分母是梯度的平方和开根号，而RMSProp的约束项的分母$- \frac{1}{\sqrt{v_t}+\epsilon}$，展开看看：

$\begin{align} v_t &= \gamma v_{t-1} + (1-\gamma)g_t^2 \\ &= \gamma (\gamma v_{t-2} + (1-\gamma) g_{t-1}^2) + (1-\gamma)g_t^2 \\ &= ... \\ &= (1-\gamma) (g_t^2 + \gamma g_{t-1}^2 + \gamma^2 g_{t-2}^2 +...+\gamma^{t-1} g_1^2 + \gamma ^t) \end{align}$

故RMSProp的约束项的分母实际上是梯度平方的指数移动平均数的开根号。故这个优化器叫做RMS。（这里指数移动平均数，就是指数加权平均，就是指数衰减平均）。

RMSProp的优点：

克服了AdaGrad的梯度急剧下降的问题，有优秀的学习率自适应能力。
在不稳定的目标函数下，表现优良。

Adadelta优化器

Adadelta和RMSProp都在约束项的分母用了梯度平方的指数移动平均数$RMS[g]_t$，不过Adadelta的全局lr不需要自己指定为$\eta$，是更新量的平方的指数加权平均数$RMS[\Delta \theta]_{t-1}$。
RMSprop和Adadelta都是为了解决Adagrad的lr急剧下降的问题。

$\theta_{t+1} = \theta_t - \frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_t}g_t$

Adam优化器

这个Adam优化器在目前很多新的通用大语言模型中很常用，很重要。
Adam是在RMSProp的基础上，加上了bias-correction，还加上了分子的一阶动量。前面几个优化器只在分母加上了梯度的梯度的二阶动量，下面是Adam的官方算法：
Adam官方算法实现过程
注意，所有向量操作是element-wise的，比如对梯度的平方，是分别对每个元素平方。