CPT cyclic precision training 论文精读

今天精读这篇论文:CPT: EFFICIENT DEEP NEURAL NETWORK TRAINING VIA CYCLIC PRECISION
官方代码在这里:github-gatech-eic-cpt

Abstract

低精度深度神经网络（DNN）训练由于减少精度是提高DNN训练时间/能量效率的最有效手段之一而受到了极大的关注。在本文中，我们尝试从一个新的角度探索低精度训练，这一角度受到最近在理解DNN训练方面的发现启发：我们推测DNN的精度在DNN训练期间可能具有类似于学习率的效果，并倡导在训练过程中使用动态精度以进一步提高DNN训练的时间/能量效率。具体来说，我们提出了循环精度训练（Cyclic Precision Training，CPT），在两个边界值之间循环变化精度，这两个边界值可以在前几轮训练中使用简单的精度范围测试来确定。对五个数据集和十一种模型进行的大量模拟和消融研究表明，CPT在各种模型/任务（包括分类和语言建模）中的有效性是一致的。此外，通过实验和可视化，我们表明CPT有助于（1）收敛到具有较低泛化误差的更宽的极小值，并且（2）减少训练方差，我们认为这为同时提高DNN训练的优化和效率开辟了一个新的设计维度。我们的代码可在以下地址获取：https://github.com/RICE-EIC/CPT

1 Introduction

现代深度神经网络（DNNs）的破纪录性能伴随着高昂的训练成本，因为需要大量的训练数据和参数，这限制了对众多应用程序高度需求的DNN驱动智能解决方案的发展（Liu等，2018；Wu等，2018）。例如，训练ResNet-50涉及10^18次浮点运算（FLOPs），在一个最先进的GPU上可能需要14天（You等，2020b）。同时，大规模的DNN训练成本引发了越来越多的财务和环境问题。例如，据估计，训练一个DNN的成本可能超过1万美元，并且排放的碳量高达一辆汽车的生命周期排放量。与此同时，最近DNN的进展激发了对智能边缘设备的巨大需求，其中许多设备需要在设备上进行现场学习，以确保在动态的现实环境中准确性，这些设备的资源有限，与高昂的训练成本之间存在不匹配（Wang等，2019b；Li等，2020；You等，2020a）。

为了应对上述挑战，广泛的研究工作致力于开发高效的DNN训练技术。其中，低精度训练引起了显著关注，因为它可以大幅提高训练时间/能量效率（Jacob等，2018；Wang等，2018a；Sun等，2019）。例如，GPU现在可以使用16位IEEE半精度浮点格式进行混合精度DNN训练（Micikevicius等，2017b）。尽管前景广阔，现有的低精度工作还没有充分利用理解DNN训练的最新发现。具体而言，现有工作大多在整个训练过程中固定模型精度，即采用静态量化策略，而最近的DNN训练优化工作建议在DNN训练过程中使用动态超参数。例如，（Li等，2019）显示，大的初始学习率有助于模型记住更易适应和更具普遍性的模式，这与从大学习率开始探索并逐渐减小以实现最终收敛的常见做法一致；（Smith，2017；Loshchilov & Hutter，2016）通过采用循环学习率提高了DNN的分类准确性。

在本文中，我们倡导动态精度训练，并作出以下贡献：

• 我们表明，DNN的精度似乎在DNN训练期间具有类似于学习率的效果，即低精度带有较大的量化噪声有助于DNN训练探索，而高精度带有更准确的更新有助于模型收敛，动态精度调度有助于DNN收敛到更好的极小值。这个发现为同时提高DNN训练的优化和效率开辟了一个设计维度。
• 我们提出了循环精度训练（Cyclic Precision Training, CPT），该方法在DNN的训练过程中采用循环精度调度，以推动DNN准确性和训练效率之间的可实现权衡。此外，我们表明，在训练的早期阶段使用简单的精度范围测试可以自动识别循环精度范围，这几乎没有计算开销。
• 在五个数据集和十一种模型上的广泛实验（包括分类和语言建模）验证了所提出的CPT技术在提高训练效率方面的一致有效性，同时达到或超过了可比的准确性。此外，我们提供了损失曲面的可视化，以更好地理解CPT的有效性，并讨论了其与最近对DNN训练优化理解的关系。

2 Related Works

量化的DNNs。DNN量化（Courbariaux等，2015；2016；Rastegari等，2016；Zhu等，2016；Li等，2016；Jacob等，2018；Mishra & Marr，2017；Mishra等，2017；Park等，2017；Zhou等，2016）已基于目标精度-效率权衡进行了深入研究。例如，Jacob等（2018）提出了量化感知训练，以保持量化后的精度；Jung等（2019）；Bhalgat等（2020）；Esser等（2019）；Park & Yoo（2020）努力使用可学习的量化器提高低精度DNN的精度。混合精度DNN量化（Wang等，2019a；Xu等，2018；Elthakeb等，2020；Zhou等，2017）为不同的层/滤波器分配不同的位宽。虽然这些工作都采用了静态量化策略，即分配的精度在量化后是固定的，但CPT在训练过程中采用了动态精度调度。

低精度DNN训练。先锋性工作（Wang等，2018a；Banner等，2018；Micikevicius等，2017a；Gupta等，2015；Sun等，2019）表明DNN可以在降低精度的情况下进行训练。对于分布式学习，（Seide等，2014；De Sa等，2017；Wen等，2017；Bernstein等，2018）量化梯度以减少通信成本，而训练计算仍然采用全精度；对于集中式/设备上的学习，前向和后向计算中涉及的权重、激活、梯度和误差都采用降低精度。我们的CPT可以应用于这些低精度训练技术之上，所有这些技术在整个训练过程中都采用静态精度，以进一步提高训练效率。

动态精度的DNNs。存在一些动态精度的工作，其目的是在全精度训练后推导出用于推理的量化DNN。具体来说，Zhuang等（2018）首先训练一个全精度模型以达到收敛，然后逐渐降低模型精度到目标值以获得更好的推理精度；Khoram & Li（2018）也从一个全精度模型开始，然后逐渐学习每一层的精度以得出一个混合精度的对应模型；Yang & Jin（2020）基于两个连续位宽的线性插值学习每一层/滤波器的分数精度，这会加倍计算并需要额外的微调步骤；Shen等（2020）提出在推理过程中以输入为依赖的方式调整每一层的精度，以平衡计算成本和精度。

3 The Proposed CPT Technique

在本节中，我们首先在第3.1节中通过可视化示例介绍推动我们开发CPT的假设，然后在第3.2节中提出CPT概念，接着在第3.3节介绍精度范围测试（PRT）方法，其中PRT旨在自动化CPT的精度调度。

3.1 CPT: Motivation

假设1：DNN的精度与学习率有类似的效果。现有研究（Grandvalet等，1997；Neelakantan等，2015）理论上或经验上表明噪声有助于DNN训练，这促使我们重新思考量化在DNN训练中的作用。我们推测，低精度和高量化噪声有助于DNN训练的探索，类似于高学习率的效果，而高精度和更准确的更新有助于模型收敛，类似于低学习率。

验证假设1。
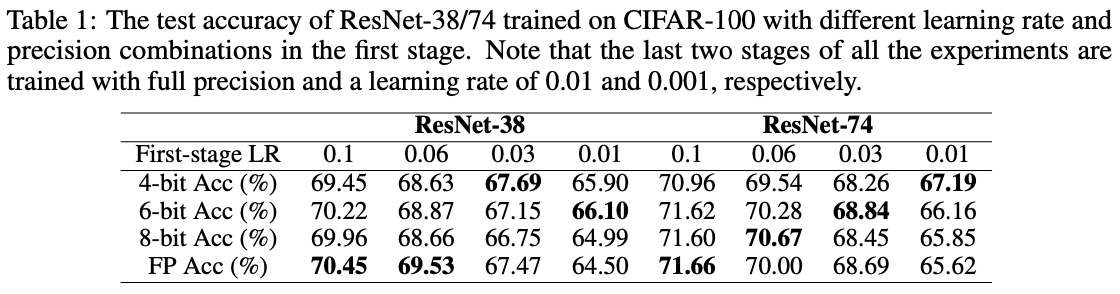
设置：为了经验性地验证我们的假设，我们在CIFAR-100数据集上训练ResNet-38/74共160个epoch，训练设置如第4.1节所述。特别是，我们将160个epoch的训练分为三个阶段：[0, 80]， [80, 120] 和 [120, 160]。在第一个训练阶段[0, 80]，我们为权重和激活采用不同的学习率和精度，而在剩下的两个阶段中使用全精度，学习率为[80, 120] epoch期间为0.01，[120, 160] epoch期间为0.001，以探索在第一个训练阶段中学习率和精度之间的关系。

结果：如表1所示，我们可以观察到，当第一个训练阶段的学习率足够降低时，采用较低精度进行训练将比使用全精度训练获得更高的准确性。特别是，在标准初始学习率为0.1的情况下，全精度训练在ResNet-38/74上分别比4位精度的训练高出1.00%/0.70%的准确性；而当初始学习率降低时，这个准确性差距逐渐缩小并反转，例如，当初始学习率降到1e-2时，在[0, 80]epoch使用4位精度训练比全精度训练高出1.40%/1.57%的准确性。

见解：这组实验表明（1）当初始学习率较低时，使用较低初始精度进行训练始终比使用全精度训练获得更好的准确性，表明降低精度引入了类似于高学习率的有利于探索的效果；（2）虽然低精度可以减轻由低学习率引起的准确性下降，但高学习率通常是最大化准确性的必要条件。

假设2：动态精度有助于DNN泛化。最近在DNN训练中的发现促使我们更好地利用DNN精度，实现DNN准确性和效率的双赢。具体来说，有讨论指出（1）DNN在不同的训练阶段学习不同的模式，例如，Rahaman等（2019）和Xu等（2019）揭示了DNN训练首先学习低频成分，然后是高频特征，前者对扰动和噪声更为鲁棒；（2）动态学习率调度有助于改善DNN训练中的优化，例如，Li等（2019）指出，大的初始学习率有助于模型记住更易适应和更具普遍性的模式，而Smith（2017）和Loshchilov & Hutter（2016）表明，循环学习率调度提高了DNN的分类准确性。这些工作激发我们假设，动态精度可能有助于DNN在优化景观中达到更好的最优解，特别是考虑到在假设1中验证的学习率和精度之间的相似效果。

验证假设2。我们的假设2已通过各种实证观察得到一致确认。例如，最近的一项工作（Fu等，2020）提出在训练过程中逐步提高精度，我们按照他们的设置验证我们的假设。

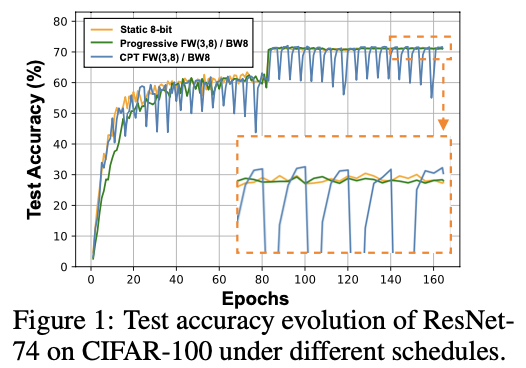
设置：我们在CIFAR-100上训练ResNet-74，训练设置与Wang等（2018b）相同，但在训练过程中量化权重、激活和梯度；对于逐步精度情况，我们在前80个epoch中将权重和激活的精度从3位均匀增加到8位，并采用静态8位梯度，而静态精度基线对所有权重/激活/梯度使用8位。

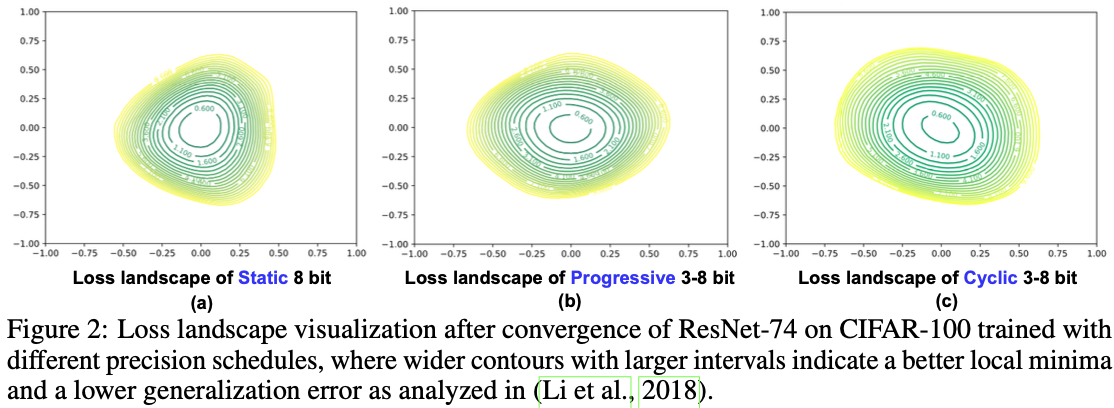
结果：图1显示，使用逐步精度调度训练的准确性略高于静态精度（+0.3%），同时前者可以降低训练成本。此外，我们在图2(b)中可视化了损失景观（按照Li等（2018）的方法）：有趣的是，逐步精度调度有助于收敛到具有更宽轮廓的更好局部极小值，这表明图2(a)中的静态8位基线具有较低的泛化误差（Li等，2018）。

Fu等（2020）中的逐步精度调度依赖于手动超参数调节。因此，一个自然的后续问题是：什么样的动态调度在不同任务/模型中既有效又易于实施？在本文中，我们表明简单的循环调度在提高训练效率的同时，始终有利于训练收敛。

3.2 CPT: The Key Concept

CPT 的关键概念受到 Li 等人 (2019) 的启发，后者表明较大的初始学习率有助于模型学习更具普遍性的模式。因此，我们假设较低的精度虽然会导致短期内较差的准确性，但由于其相关的较大量化噪声，实际上可能有助于 DNN 训练期间的探索；同时众所周知，较高的精度可以学习更高复杂度和细粒度的模式，这对于更好的收敛至关重要。两者结合可能会改善最终的准确性，因为它可能在 DNN 训练过程中更好地平衡粗粒度探索和细粒度优化，这就是 CPT 的理念。
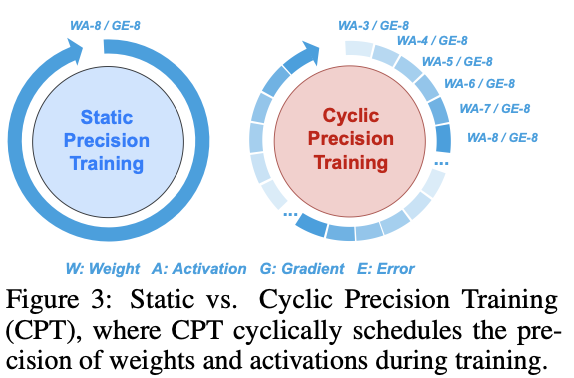
具体而言，如图 3 所示，CPT 在两个边界之间循环变化精度，而不是在训练过程中固定精度，从而让模型以不同的粒度探索优化景观。

虽然 CPT 可以使用不同的循环调度方法实现，这里我们以余弦方式的实现作为示例：

$$B_t^n = \lceil B_{min}^n + \frac{1}{2} (B_{max}^n - B_{min}^n)(1-cos(\frac{t \% T_n}{T_n} \pi)) \rfloor$$

其中$B_{min}^n$ $B_{max}^n$分别是第n个周期精度调度中的下限和上限精度，⌈⋅⌋ 和 $\%$ 分别表示取整运算和取余运算，$B_{tn}$ 是在第t个全局epoch中第n个周期的精度，周期长度为 $T_n$。注意，周期长度 $T_n$ 等于总训练epoch数除以周期总数 $N$，其中 $N$ 是CPT的超参数。例如，如果 $N = 2$，那么在训练过程中，使用CPT的DNN训练将经历两个循环精度调度周期。如第4.3节所示，我们发现采用不同数量的循环精度调度周期进行训练时，CPT的好处是保持不变的，即CPT对 $N$ 不敏感。精度调度的可视化示例见附录A。此外，我们发现使用不同的动态精度调度模式（即，不一定是公式(1)中的余弦调度）时，CPT通常是有效的。在本工作中，我们按照公式(1)实现CPT，并在第4.3节讨论了可能的变体。

我们在图1中可视化了CPT在ResNet-74上的训练曲线（使用CIFAR-100数据集），发现与静态固定精度的对应方法相比，CPT提高了0.91%的准确性，并减少了36.7%的所需训练BitOPs（位操作）。此外，图2 (c) 可视化了相应的损失景观，显示了CPT的有效性，即这种简单且自动化的精度调度导致了更好的收敛和更低的尖锐度。

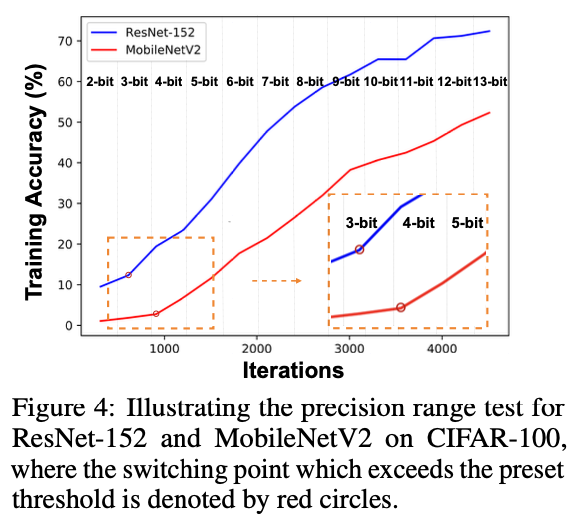
3.3 CPT: Precision Range Test

CPT 的概念足够简单，可以插入到任何模型或任务中以提高训练效率。一个剩下的问题是如何确定精度边界，即公式(1)中的 $B^i_{\text{min}}$ 和 $B^i_{\text{max}}$，我们发现可以在精度调度的第一个周期（即 $T_i = T_0$）中使用简单的PRT以几乎可忽略的计算成本自动决定。具体来说，PRT 从最低可能的精度（例如2位）开始，并逐渐增加精度，同时监控几个连续迭代中训练准确性幅度的变化；一旦这种训练准确性差异超过预设阈值，表明训练至少部分收敛，PRT 将确认下限精度已确定。虽然上限精度也可以类似地确定，但存在一种替代方法，建议简单采用CPT的静态精度对应方法的精度。其余周期使用相同的精度边界。

图4 可视化了在 CIFAR-100 上训练的 ResNet-152/MobileNetV2 的 PRT。我们可以看到，当模型在 ResNet-152 上经历显著的训练准确性提高时确定的最低精度边界是3位，而 MobileNetV2 是4位，这与常见观察一致，即 ResNet-152 对量化的鲁棒性比更紧凑的模型 MobileNetV2 更强。

4 Experiment Results

在本节中，我们将首先在第4.1节描述实验设置，在第4.2节展示在各种任务中基准测试SOTA训练方法的结果，然后在第4.3节进行CPT的全面消融研究。

4.1 Experiment Setup

模型、数据集和基线。我们考虑了十一种模型（包括八种基于ResNet的模型（He等，2016）、MobileNetV2（Sandler等，2018）、Transformer（Vaswani等，2017）和LSTM（Hochreiter & Schmidhuber，1997））和五个任务（包括CIFAR-10/100（Krizhevsky等，2009）、ImageNet（Deng等，2009）、WikiText-103（Merity等，2016）和Penn Treebank（PTB）（Marcus等，1993））。具体来说，我们按照Wang等（2019b）的方法在CIFAR-10/100上实现MobileNetV2。

基线：我们首先在三种SOTA静态低精度训练技术上对CPT进行了基准测试：SBM（Banner等，2018）、DoReFa（Zhou等，2016）和WAGEUBN（Yang等，2020），每种技术都采用了不同的量化器。由于SBM在报告的结果和我们的实验结果中都是最具竞争力的基线，因此我们在SBM的基础上应用了CPT，除非特别说明，所有的静态精度基线都采用SBM量化器。另一个基线是在静态精度训练的基础上采用的循环学习率（CLR）（Loshchilov & Hutter，2016），我们遵循了Loshchilov & Hutter（2016）中的最佳设置。

训练设置：我们在所有实验中都遵循标准的训练设置。特别是，对于分类任务，我们分别按照Wang等（2018b）在CIFAR-10/100上的SOTA设置和He等（2016）在ImageNet实验中的设置进行；对于语言建模任务，我们遵循Baevski & Auli（2018）在WikiText-103上使用Transformer的方法和Merity等（2017）在PTB上使用LSTM的方法。

精度设置：所有实验中的低精度边界使用第3.3节中的PRT设置，上限精度与相应静态精度基线的精度相同。我们仅将CPT应用于权重和激活（统称为FW），而误差和梯度使用静态精度（统称为BW），后者是为了确保梯度的稳定性（Wang等，2018a）（更多讨论见附录C）。特别地，CPT从3位到8位的权重和激活，使用8位梯度，记为FW(3,8)/BW8。所有实验中的周期性精度循环总数，即第3.3节中的N，固定为32（见第4.3节中的消融研究）。

硬件设置和指标：为了验证所提出的CPT的实际硬件效率，我们采用了标准的FPGA实现流程。具体来说，我们使用Vivado HLx设计流程在名为ZC706（Xilinx）的Xilinx开发板上实现基于FPGA的加速器。为了更好地评估训练成本，我们考虑了计算的GBitOPs（Giga bit operations）和在ZC706 FPGA板上的实际测量延迟。

4.2 Benchmark with SOTA Static Precision Training Methods

CIFAR-10/100上的基准测试。基于SOTA量化器的基准测试：我们在训练ResNet-74/164和MobileNetV2于CIFAR-10/100时，使用三种SOTA静态低精度训练方法对CPT进行基准测试，如表2所总结的，涵盖了代表性低精度DNN训练中深度和紧凑的DNN。需要注意的是，精度提升是指在相同设置下CPT与最强基线之间的差异。表2显示，（1）我们的CPT在CIFAR-10/100的所有情况下，始终实现了更高的精度（+0.19%~+1.25%）和更低的训练成本（-21.0%~ -37.1%的计算成本和-14.7%~ -21.4%的延迟），即使是紧凑模型MobileNetV2，（2）在极低精度下，CPT在精度方面显著优于基线，这是低精度DNN训练中最有用的场景之一。特别是，CPT在4位和6位之间的周期性精度训练，相比于CIFAR-10上的静态6位训练，在ResNet-74/164上分别提高了1.25%和1.07%的精度，验证了CPT导致了更好的收敛。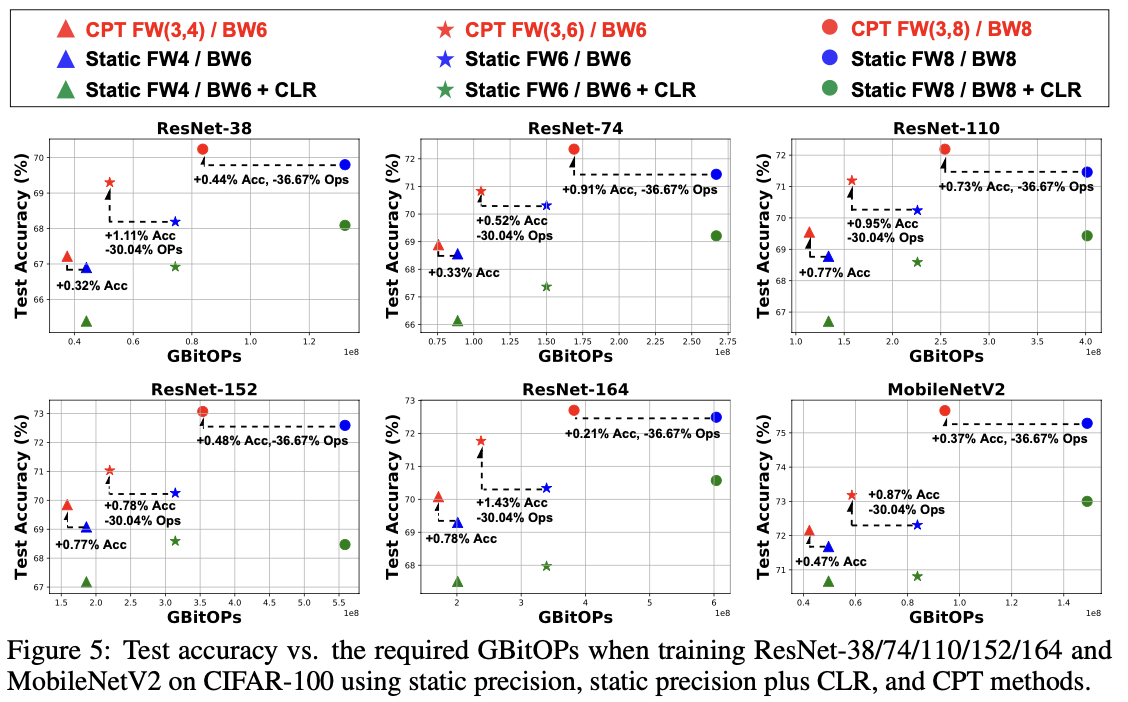

基于SBM之上的CLR基准测试：我们进一步在SBM之上用CLR（Loshchilov & Hutter, 2016）对CPT进行基准测试（继承其在CIFAR-100上的最佳设置），如表2所示，SBM在SOTA量化器中表现最好，如图5所示，基于更多的DNN模型和精度。我们可以看到，（1）CPT仍然始终以更好的精度和效率权衡优于所有基线，（2）SBM之上的CLR对测试精度产生负面影响，我们推测这是由于低精度训练下梯度的不稳定性和对学习率的敏感性（Wang等，2018a所讨论），显示CPT比CLR更适用于低精度训练。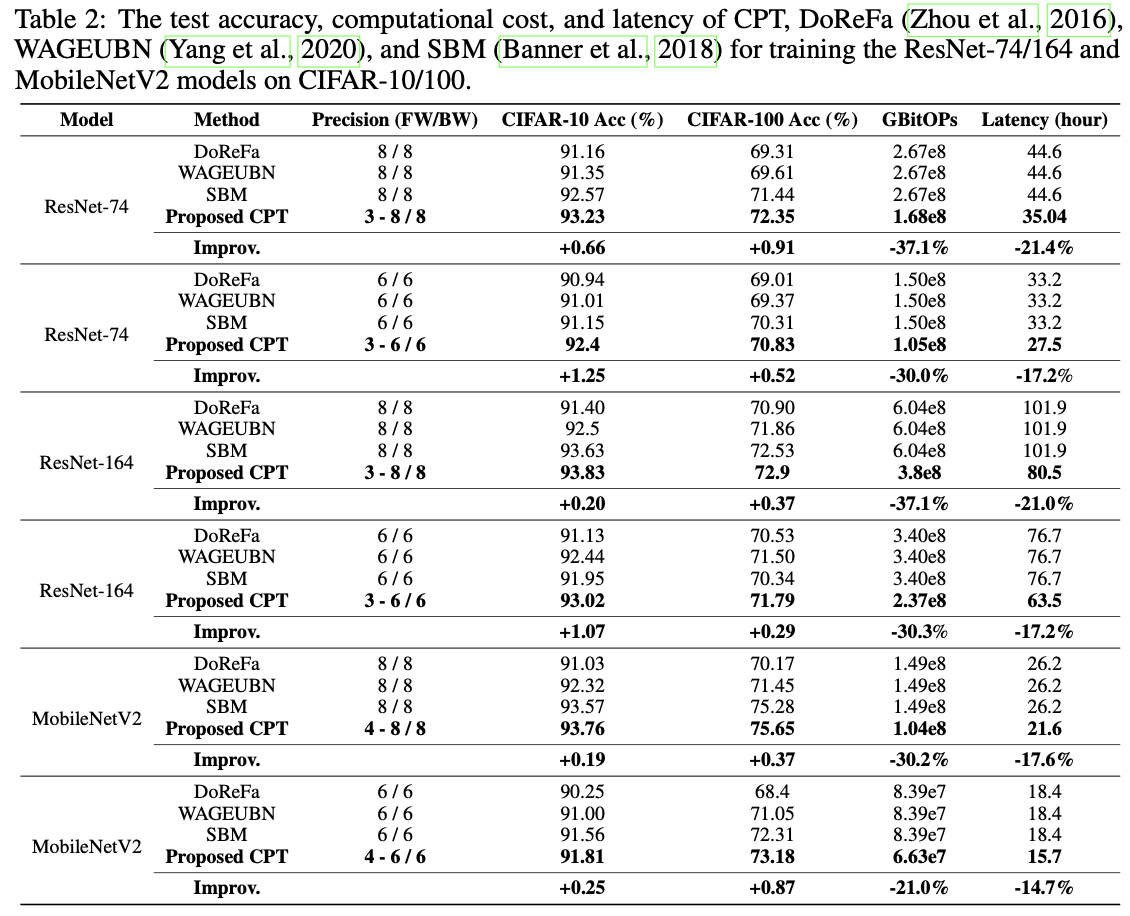

损失景观可视化：为了更好地理解CPT实现的卓越性能，我们按照Li等（2018）的方法可视化了损失景观，如图6所示，涵盖了非紧凑和紧凑模型以及低精度设置（即6位和8位），这是低精度DNN训练的瓶颈。我们可以观察到，使用CPT训练的标准和紧凑DNN都经历了更宽的轮廓和更少的尖锐度，表明CPT有助于DNN训练优化收敛到更好的局部最优。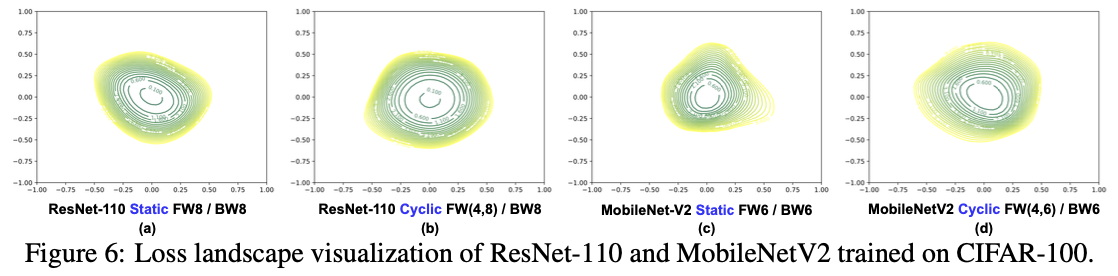

ImageNet上的基准测试。为了验证CPT在更复杂任务和更大模型上的可扩展性，我们在ImageNet上的ResNet-18/34/50上使用SOTA静态精度训练方法SBM（Banner等，2018）进行基准测试，在这种情况下，低精度训练如4位的工作具有挑战性。如表3所示，我们可以观察到CPT仍然在计算成本减少的情况下（最多-30.4%）实现了可比的精度（-0.20%~+0.06%）。特别是，CPT在ResNet-50上表现良好，既提高了精度，又提高了训练效率，表明CPT在模型复杂性上的可扩展性，因此除了设备上的训练场景外，它还有潜在的应用于大规模训练的可能性。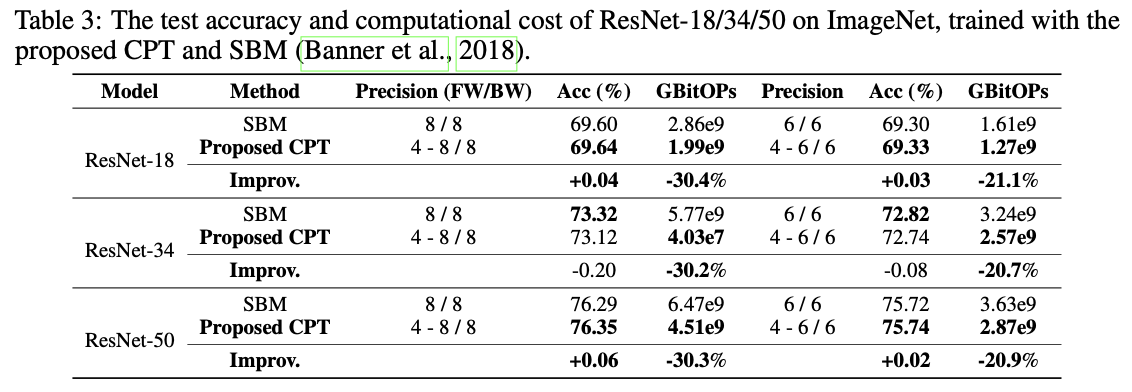

CPT提升精度：CPT的一个重要方面是其在提高训练优化方面的潜力。我们通过在ImageNet上使用CPT和静态全精度训练ResNet-18/34来说明CPT在提高最终精度方面的优势。如表4所示，CPT在ResNet-18/34上分别比其全精度对应模型在ImageNet上提高了0.91%/0.84%的精度，表明CPT不仅可以作为提高训练效率的一般技术，还可以提高最终精度。

WikiText-103和PTB上的基准测试。我们还将CPT应用于语言建模任务（包括WikiText-103和PTB）（见表5），以表明CPT也适用于自然语言处理模型。表5显示，（1）CPT在精度（即困惑度——越低越好）和训练效率方面始终实现了双赢，（2）语言建模模型/任务对量化更敏感，尤其是在LSTM模型中，因为它总是适应较大的低精度边界，这与SOTA的观察一致（Hou等，2019）。

4.3 Ablation Studies of CPT

CPT 在不同精度范围内的表现。我们还评估了CPT在不同的上限精度范围内的表现，这些范围对应于不同的目标效率，以查看CPT是否仍然表现良好。图7展示了每次实验重复十次的箱线图。我们可以看到，（1）无论采用何种精度范围，CPT始终实现了双赢（+0.74% ∼ +2.03%的更高准确性和-18.3% ∼ -48.0%的计算成本减少），特别是在低精度场景下，（2）CPT甚至缩小了准确性方差，这更符合高效训练的实际目标。

CPT 在不同精度调度周期数下的表现。为了评估CPT对采用的循环精度调度周期总数的敏感性，我们在不同的调度周期数下将CPT应用于ResNet-38/74和CIFAR-100。图8展示了基于十次重复实验的平均准确性。我们可以看到，（1）不同的周期总数选择在CIFAR-10/100上导致了可比的准确性（在0.5%以内）；（2）CPT在不同精度调度周期数下在达到的准确性上始终优于静态基线SBM。基于这个实验，我们为简化起见，将 $N = 32$ 设为固定值。

CPT 在不同循环精度调度模式下的表现。除了余弦调度模式外，我们还使用其他循环精度调度模式评估了CPT，包括由Smith（2017）提出的三角形调度模式和作为学习率调度的余弦退火调度（Loshchilov & Hutter，2016），所有这些模式都采用32个循环周期以保持公平。表6中的实验表明，（1）CPT在不同调度模式下始终有效；（2）在某些情况下，CPT使用其他两个调度模式甚至超越了余弦调度模式，但在紧凑模型上表现不佳。如何为给定模型和任务确定最佳的循环模式留作未来的研究工作。

5 Discussions about Future Work

CPT 的理论视角。近年来，对理解和优化 DNN 训练的兴趣日益浓厚。例如，Li 等人（2019）显示，使用较大的初始学习率训练 DNN 有助于模型更快更好地记住更具普遍性的模式。最近，Zhu 等人（2020）显示，在凸性假设下，低精度 DNN 训练的收敛界由量化噪声和学习率的线性组合决定。关于 DNN 训练的这些发现似乎与我们 CPT 的有效性一致。

CPT 的硬件支持。最近在支持动态精度的混合精度 DNN 加速器（Lee 等，2019；Kim 等，2020）中的进展有望支持我们的 CPT。我们将 CPT 的最佳加速器设计留作未来的研究工作。

6 Conclusion

我们假设，在 DNN 训练中，DNN 的精度具有与学习率类似的效果，即低精度和高量化噪声有助于 DNN 训练的探索，而高精度和更准确的更新有助于模型收敛，因此主张动态精度调度有助于 DNN 训练优化。然后，我们提出了 CPT 框架，该框架采用周期性精度调度进行低精度 DNN 训练，以提升任务准确性和训练效率的可实现帕累托前沿。大量实验和消融研究验证了 CPT 可以在训练期间降低计算成本，同时实现可比或更高的准确性。我们的未来工作将努力找到更多这种动态低精度训练的理论依据。