常见损失函数介绍

常见损失函数

损失函数就是用于计算预测label和真实label之间差距的函数.

MSE损失函数

MSE是mean squared error, 均方误差损失函数. 求两个向量的差的平方之和, 再对batch size=n求均值. 公式如下:

$$MSE = \frac{1}{n}\sum_{i=1}^n(\hat y_i - y_i)^2=\frac{1}{n}\sum_{i=1}^n(\sum_{j=1}^M(\hat y_i^j - y_i^j)^2)$$

其中$y_i$是真实label向量, 是$\hat y_i$预测label向量, 向量大小是1*m, batch size=n.
如果batch size=1, 就是真实向量和预测向量的对应元素之差的平方, 再对所有m个位置求和.

MSE特点:

• 损失函数的曲线光滑可导, 随着误差的减小, 梯度也减小, 利于函数收敛.
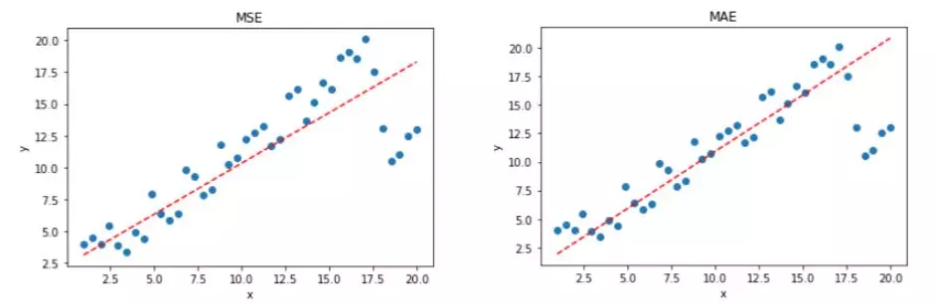
• 平方项, 对大误差有大的惩罚力度, 对小误差有小的惩罚力度.
• 如果样本中有离群点, MSE会给离群点赋予更高的权重，但是却是以牺牲其他正常数据点的预测效果为代价，这最终会降低模型的整体性能。

MAE平均绝对误差

MAE: Mean absolute error,

$$MAE = \frac{1}{n} \sum_{i=1}^n |\hat y_i - y_i |$$

其中$y_i$是真实label向量, 是$\hat y_i$预测label向量, batch size=n. 向量对应元素之差的绝对值求和, 再在batch size维度求平均值.

特点:

• 曲线呈现V形状，连续但在$\hat y_i - y_i =0$处不可导，计算机求解导数比较困难。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。
• 对离群点不敏感。没有平方项，惩罚力度一样。而MSE对离群点敏感。
  

CE交叉熵损失函数

CE: cross entropy loss, 公式:

$$L=-\frac{1}{n}\sum_i y_i \log p_i =-\frac{1}{n}\sum_i \sum_{j=1}^m y_i^j \log p_i^j$$

其中batch size=n, m是分类数 即向量是1*m大小的. $y_i$是真实向量, $p_i$是预测向量. $y_i^j$表示向量的第j个元素.

经常会提到CE和最大似然法的关系, 在面试中也可能问道. 什么事最大似然法, 以及CE和它到底有什么关系? 具体看这个博客: 最大似然估计和CE的关系

infoNCE损失函数

infoNCE和CE loss很像. infoNCE在MoCo论文当中使用, 是无监督对比学习方法用到的损失函数. 公式:

$$L_q = - \log \frac{e^{q\cdot k_{+} / \tau }}{\sum_{i=0}^K e^{q\cdot k_i/\tau}}$$

其中q和k+互为正样本对, 是从同一个图片经过不同图片增强得到的向量, q和k-互为负样本对, 是不同图片对应的向量. 一共有K个k- (negative key).
用向量点乘(对应元素之积的和)表示两个向量的相似性, 如分子中的$q\cdot k_{+}$越大表示这个正样本对越相似, 分母中是K个负样本对的点乘之和加上$q\cdot k_{+}$, 分母一共有K+1项.
其中$\tau$是温度系数.

CE和infoNCE的区别:

在计算交叉熵损失函数CE之前, 一般会让预测向量经过一个softmax变为概率预测向量, 如果是一个K+1分类问题, 真实label向量形如$y=[1,0,0…,0]$, 而预测向量形如$\hat y = [y^0, y^1, …, y^{K}]$, 经过softmax后

$$p=softmax(\hat y) = [\frac{e^{y^0}}{\sum e^{y^i}},\frac{e^{y^1}}{\sum e^{y^i}}, ..., \frac{e^{y^K}}{\sum e^{y^i}} ]$$

假设batch size=1, 求CE:

$$H(y, p) = - \sum_{i=0}^K y^i \log p^i = - log p^0 =- \log \frac{e^{y^0}}{\sum_{i=0}^K e^{y^i}}$$

和上面的infoNCE公式很像.

CE和infoNCE的区别:
CE中, 真实向量是一个one-hot向量, 长度是分类数.

无监督的对比学习没有真实label向量, 所以infoNCE中的K不是分类数, 而是表示的negative key的个数, 用长度为K的queue来存储负样本向量k-.

infoNCE可以看做特殊的CE, 即分类数为K+1, 且真实类别是index=0处的分类任务.

总结一下, CE和infoNCE的区别:

• CE用于分类任务时, 是有标签数据, K表示类别数; 而infoNCE用于无监督的对比学习, 是无标签数据, K表示negtive key的个数.
• infoNCE把k+和K个k-向量拼起来, k+在index=0的位置, 得到长度为K+1的序列, 可以理解为: 真实类别为0的K+1分类任务.

温度系数$\tau$的作用:
$\tau$是超参数, 很重要. 温度系数用于控制预测向量logits的分布形状.

如果$\tau$很大, 则$q\cdot k / \tau$变小, logits分布变平滑, 对比损失函数对所有负样本一视同仁, 不会特别关注某个负样本, 模型的学习没有轻重.

相反地，如果$\tau$变小，logits分布的值$q\cdot k / \tau$变大，分布变得更不均匀，更peak。模型会特别关注困难的负样本（也就是$q\cdot k$更大的样本对，也就是潜在的正样本对），导致模型收敛困难，泛化能力差。

总之，温度系数的作用就是它控制了模型对负样本的区分度。